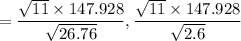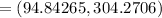Solution :
a). Given :
a =
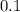 ,
,
chisquare with the
 ,
,
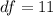 is
is
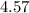 (from the chisquare table)
(from the chisquare table)
Chisquare with the
 , df =
, df =
 is
is
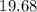 (from chisquare table)
(from chisquare table)
So 90% Cl is

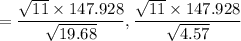
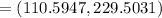
b). Given :
a =

Chisquare with
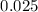
df =
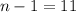 is A,
is A,

Chisquare with
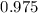 , df = 11 is
, df = 11 is
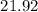
So, 95% Cl is

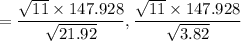

c). Given a =
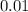 , chisquare with
, chisquare with
 , df =
, df =
 is
is
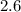
Chisquare with
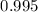 , df =
, df =
 is
is
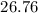
So 99% CI is