Question

Can someone help me solve this problem?

Answer 1

a = 8

b = 4
`√(2)`

Explanation:

I've attached a picture of the 45-45-90 triangle's formula, which is the length of the hypotenuse =
`√(2)` times the length of a leg (one of the sides of the triangle).

So, applying this to your problem, if 4
`√(2)` if one of the legs of the triangle, the other leg, which is b , would be the same length.

b = 4
`√(2)`

To solve for a, you would have to multiply the leg by
`√(2)`.

a = 4
`√(2)` x
`√(2)`

I would separate the 4 and the
`√(2)`.

a = 4 x
`√(2)` x
`√(2)`

a = 4 x
`√(2 *2)`

a = 4 x
`√(4)`

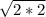
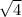
a = 4 x 2

a= 8