Question

Write an equation in point slope form of the line with the given characteristics.

1. Parallel to the line y=3/5x-8; passes through (0,-3)

2. Perpendicular to the line y=-2x-7; passes through (-3,10)

Answer 1

1. y + 3 = 3/5(x)

2. y - 10 =
`(1)/(2)`(x + 3)

Explanation:

1.

When a line is parallel to another line, it means that the two lines have the same slope. So, for this first problem, the slope of the other parallel line would have to be 3/5.

In the problem, they've given you a point of (0, -3).

Now, you can can plug everything you know into the point slope formula which is...

y -
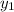`y_(1)` = m ( x -
`x_(1)`).

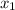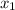`x_(1)` and
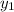`y_(1)` are the points that you plug in, and m is the slope.

After you plug everything in, you should get:

y + 3 = 3/5(x + 0)

You don't really need to include the 0, so your final equation would be

y + 3 = 3/5(x).

2.

When a line is perpendicular to another line, it means that the slope of the other is its opposite reciprocal. This means that the slope of the perpendicular line would be 1/2. I got this by dividing 2 by 1 and multiplying it by -1.

reciprocal of -2 = -
`(1)/(2)` x -1 =

You can do the same thing we did in the previous problem with the point given here, which is (-3, 10).

y - 10 =
`(1)/(2)`(x + 3)