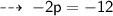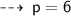Given :
- If one root of the equation x²+ px + 8 = 0 is -2, then find the value of p.
Understanding the question :
- Here, In this question, it is given the root of the equation which means we have the value of x.
- Now we are to put the value of x which is (-2) and by evaluating it we could find the value of p.

Solution :

Now putting the value of x in the equation :
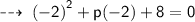
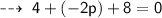
Adding the like terms :
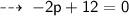
Transposing 12 to the right side thus it becomes negative :
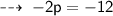
Cancelling (-) from both sides :