Ordered from least to greatest, the numbers are:
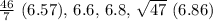 .
.
To compare and order the numbers from least to greatest, follow these steps:
1. Simplify the Square Root: First, we need to simplify the square root of 47. Since 47 is not a perfect square, we'll need to find the two perfect squares it lies between. We know that
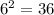 and
and
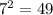 . So,
. So,
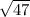 is between 6 and 7, but closer to 7 because 47 is closer to 49.
is between 6 and 7, but closer to 7 because 47 is closer to 49.
2. Divide 46 by 7: Next, we divide 46 by 7 to get an exact decimal. This will help us to compare it with the other decimals.
3. List the Numbers: The numbers given are 6.6,
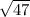 ,
,
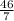 , and 6.8.
, and 6.8.
4. Compare and Order: We need to compare these numbers to place them in order from least to greatest.
Let's perform the calculations for steps 1 and 2.
The square root of 47 is approximately 6.86, and 46 divided by 7 is approximately 6.57.
Now we have all the numbers in decimal form:
- 6.6
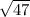 ≈ 6.86
≈ 6.86
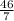 ≈ 6.57
≈ 6.57- 6.8
To plot these numbers on the number line, you would place:
-
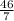 (6.57) just a little past the midpoint between 6.5 and 6.6.
(6.57) just a little past the midpoint between 6.5 and 6.6. - 6.6 directly above the corresponding point on the number line.
- 6.8 directly above the corresponding point on the number line.
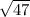 (6.86) just a little before 6.9 on the number line.
(6.86) just a little before 6.9 on the number line.
The exact positions would depend on the scale of the number line, but these approximations should help you visualize their placement.