Question

A population of rabbits in a lab, p(x), can be modeled by the function p(x)=20(1.014)^x, where x represents the number of days since the population was first counted.

Answer 1

(a) 20 represents the initial population and

1.014 represents 1 + % growth of rabbits each day

(b) Average Rate of change = 0.8

Explanation:

P.S - The exact question is -

Given - A population of rabbits in a lab, p(x), can be modeled by

the function p(x)=20(1.014)^x, where x represents the number

of days since the population was first counted.

To find - (a) Explain what 20 and 1.014 represent in the context of

the problem.

(b) Determine, to the nearest tenth, the average rate of

change from day 50 to day 100.

Proof -

(a)

Given that the function p(x) is represented as

`p(x) = 20(1.014)^(x)`

Here,

20 represents the initial population and

1.014 represents 1 + % growth of rabbits each day

(b)

Given,

`p(x) = 20(1.014)^(x)`

When x = 50

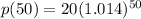`p(50) = 20(1.014)^(50)` = 40.08000 ≈ 40.1

When x = 100

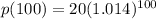`p(100) = 20(1.014)^(100)` = 80.32033 ≈ 80.3

Now,

Average Rate of change =
`(p(100) - p(50))/(100 - 50)`

=
`(80.3 - 40.1)/(50)`

=
`(40.2)/(50)`

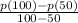
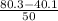
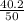
= 0.804 ≈ 0.8

⇒Average Rate of change = 0.8