We are given with a square matrix and we are asked to find it's inverse if it exists . So , let's recall some important points first :-
- Inverse can only be found of square matrices.
- If
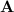 is a square matrix than , it's inverse is denoted by
is a square matrix than , it's inverse is denoted by
 , and is given by
, and is given by
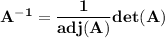 , where adj(A) is the adjoint of the matrix A and det(A) is the determinant of the matrix A
, where adj(A) is the adjoint of the matrix A and det(A) is the determinant of the matrix A
- Inverse of a matrix exist if A is non-singular
- Non-Singular means that det(A) ≠ 0
- Adjoint of a matrix is the matrix of transpose of cofactors
- Transpose of a matrix is founded by exchanging it's rows by columns and columns by rows and is denoted by
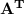
Now , in this question let's assume that
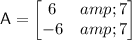
Now , Calculating det(A) :-
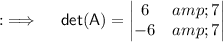
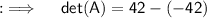
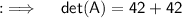
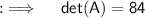
As , det(A) ≠ 0 . So ,
 exists . Now , we need to find the matrix of cofactors first , but let's find cofactors first , so here ;
exists . Now , we need to find the matrix of cofactors first , but let's find cofactors first , so here ;
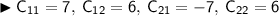
Now , let's assume that matrix of cofactors is C , so putting the cofactors as elements of the matrix , C will be ;
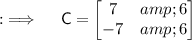
Now , adj(A) will be found by interchanging it's rows by columns and vice versa.
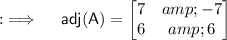
Now as
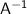 is given by
is given by
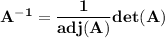
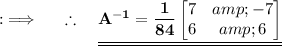
Hence , Option C)
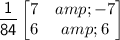 is correct :D
is correct :D