Answer:
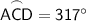
Explanation:
A Major arc is an arc that is larger than a semicircle and is named by three points. The first and third points are the endpoints of the arc, and the middle point is any point on the arc between the two endpoints.
The degree measure of an arc equals the measure of its corresponding central angle.
To find the measure of a major arc, subtract the minor arc that has the same endpoints as the major arc from 360°.
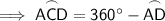
To find the arc measure of the minor arc AD, find the value of x:
Angles on a straight line sum to 180°
⇒ m∠APD + m∠DPC + m∠CPB = 180°
⇒ (7x + 1)° + 90° + (9x - 7)° = 180°
⇒ 7x + 1 + 9x - 7 = 90°
⇒ 16x - 6 = 90°
⇒ 16x = 96°
⇒ x = 6
Substitute the found value of x into the expression for m∠APD:
⇒ m∠APD = 7x + 1
⇒ m∠APD = 7(6) + 1
⇒ m∠APD = 42 + 1
⇒ m∠APD = 43°
Therefore,
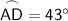
Finally, substitute the found value of minor arc AD into the equation:
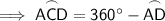
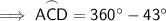
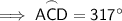
Therefore, the arc measure of major arc ACD is 317°.