Question

In a recent academic year, many public universities in the United States raised tuition and fees due to a decrease in state subsidies. The change in the cost of tuition, a shared dormitory room, and the most popular meal plan from the previous academic year for a sample of 10 public universities were as follows:

$1,589, $593, $1,223, $869, $423, $1,720, $708, $1,425, $922 and $308.

a. What is the mean and median change in the cost? (Explain how you obtain your answer.)
b. What is the five-number summary of the change in the cost? (Explain how you obtain your answer.)
c. What is the standard deviation of the change in the cost? (Explain how you obtain your answer.)
d. The middle 50% of the change in the cost is spread over what value? (Explain how you obtain your answer.)
e. What is the coefficient of variation of the change in cost? (Explain how you obtain your answer.)
f. What are the (absolute values of) the Z scores of the change in cost?

Answer 1

1. mean = 980 median = $895.5

2. 308, 593, 895.5, 1425, 1720

3. 491.7978

4. 895.5

5. 50.28%

Explanation:

1. mean $1,589+$593+$1,223+$869+$423+$1,720+$708+$1,425+$922+$308/10

= 9780/10

= $978

median

We first arrange the values in ascending order

308,423,593,708,869,922,1223,1425,1589,1720

number of observation is even so we pick the 2 values in the middle and divide by 2

= 869+922/2

= $1791/2

$895.5

2. five number summary of change

the botom half of th dta set = 308,423,593,708,869

minimum value = 308

n = 5

median = 593 = q1

from 1, q2 = median = $895.5

the upper half of data

922,1223,1425,1589,1720

n = 5

median = $1425

maximum value = $1720

the five number summary of change in cost is therefore

308, 593, 895.5, 1425, 1720

3. standard deviation

`s =[√(x-barx) ]^(2) (1)/(n-1)`

bar x is the mean = 978

($1,589-978)²+ ($593-978)²+ ($1,223-978)²+ ($869-978)+ ($423-978)²+ $1,720-978)²+($708-978)²+ ($1,425-978)²+ ($922-978)²+ ($308-978)²

= 2176786

=
`\sqrt(1)/(10-1) {2176786} \\\sqrt{ (2176786)/(9)`

=
`√(241865.1)`

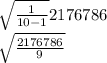
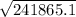
= 491.7978

4. middle 50% is spread over the median, which is 895.5

5. coefficient of variation

= s/bar x * 100

= 491.7978/978 * 100

= 49179.78/978

= 50.28%

6. z score = x - mean/s

x = 1589

= 1589-978/491.7978

= 1.2424

for x = 593

593-978/491.7978

= -0.7828

= 0.7828

for x = 1223

1223-978/491.7978

= 0.4982

for x = 869

869-978/491.7978

= -0.2216

= 0.2216

for x = 423

423-978/491.7978

= -1.1285

= 1.1285

x = 1720

1720-978/491.7978

z = 1.5088

for x = 708

708-978/491.7978

= -0.5490

= 0.5490

for x = 1425

1425-978/491.7978

= 0.9089

for x = 922

922-978/491.7978

= -0.1139

= 0.1139

for x = 308

308-978/491.7978

= -1.3624

= 1.3624