Question

A train consists of a 50 Mg engine and three cars, each having a mass of 30 Mg . If it takes 75 s for the train to increase its speed uniformly to 45 km/h , starting from rest, determine the force T, developed at the coupling between the engine E and the first car A. The wheels of the engine provide a resultant frictional tractive force F which gives the train forward motion, whereas the car wheels roll freely. Also, determine F acting on the engine wheels.

Answer 1

T = 15 kN

F = 23.33 kN

Step-by-step explanation:

Given the data in the question,

We apply the impulse momentum principle on the total system,

mv₁ + ∑
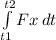`\int\limits^(t2)_(t1) {Fx} \, dt` = mv₂

we substitute

[50 + 3(30)]×10³ × 0 + FΔt = [50 + 3(30)]×10³ × ( 45 × 1000 / 3600 )

F( 75 - 0 ) = 1.75 × 10⁶

The resultant frictional tractive force F is will then be;

F = 1.75 × 10⁶ / 75

F = 23333.33 N

F = 23.33 kN

Applying the impulse momentum principle on the three cars;

mv₁ + ∑
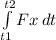`\int\limits^(t2)_(t1) {Fx} \, dt` = mv₂

[3(30)]×10³ × 0 + FΔt = [3(30)]×10³ × ( 45 × 1000 / 3600 )

F(75-0) = 1.125 × 10⁶

The force T developed is then;

T = 1.125 × 10⁶ / 75

T = 15000 N

T = 15 kN