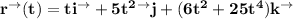Question

Find a vector function, r(t), that represents the curve of intersection of the two surfaces. The paraboloid z = 6x2 + y2 and the parabolic cylinder y = 5x2.

Answer 1

`\mathbf{r^(\to) (t) = ti^(\to) + 5t^2^(\to) j+(6t^2 + 25t^4) k ^(\to)}`

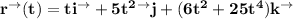
Explanation:

Given that:

The paraboloid surface z = 6x² + y² and the parabolic cylinder y = 5x²

Let assume that:

x = t

then from y = 5x², we have:

y = 5t²

Now replace y = 5t² and x = t into z = 6x² + y²

z = 6t² + (5t²)²

z = 6t² + 25t⁴

Hence, the curve of intersection is illustrated by the set of equations:

x = t, y = 5t², and z = 6t² + 25t⁴

As a vector equation:

`\mathbf{r^(\to) (t) = ti^(\to) + 5t^2^(\to) j+(6t^2 + 25t^4) k ^(\to)}`