Question

For each​ situation, identify the sample size​ n, the probability of a success​ p, and the number of successes x. When asked for the​ probability, state the answer in the form​ b(n,p,x). There is no need to give the numerical value of the probability. Assume the conditions for a binomial experiment are satisfied. Complete parts​ (a) and​ (b) below.

Required:
a. A 2017 poll found that 53% of college students were very confident that their major will lead to a good job. If 30 college students are chosen at random, what's the probability that 14 of them were very confident their major would lead to a good job?
b. A 2017 poll found that 53% of college students were very confident that their major will lead to a good job. If 30 college students are chosen at random, what's the probability that 10 of them are NOT confident that their major would lead to a good job?

Answer 1

a) 0.1138 = 11.38% probability that 14 of them were very confident their major would lead to a good job

b) 0.0483 = 4.83% probability that 10 of them are NOT confident that their major would lead to a good job

Explanation:

Binomial probability distribution

The binomial probability is the probability of exactly x successes on n repeated trials, and X can only have two outcomes.

`P(X = x) = C_(n,x).p^(x).(1-p)^(n-x)`

In which
`C_(n,x)` is the number of different combinations of x objects from a set of n elements, given by the following formula.

`C_(n,x) = (n!)/(x!(n-x)!)`

And p is the probability of X happening.

a. A 2017 poll found that 53% of college students were very confident that their major will lead to a good job. If 30 college students are chosen at random, what's the probability that 14 of them were very confident their major would lead to a good job?

Here, we have that
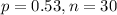`p = 0.53, n = 30`, and we want to find
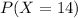`P(X = 14)`. So

`P(X = x) = C_(n,x).p^(x).(1-p)^(n-x)`

`P(X = 14) = C_(30,14).(0.53)^(14).(0.47)^(16) = 0.1138`

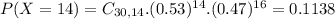
0.1138 = 11.38% probability that 14 of them were very confident their major would lead to a good job.

b. A 2017 poll found that 53% of college students were very confident that their major will lead to a good job. If 30 college students are chosen at random, what's the probability that 10 of them are NOT confident that their major would lead to a good job?

10 not confident, so 30 - 10 = 20 confident. This is P(X = 20).

`P(X = x) = C_(n,x).p^(x).(1-p)^(n-x)`

`P(X = 20) = C_(30,20).(0.53)^(20).(0.47)^(10) = 0.0483`

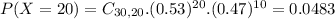
0.0483 = 4.83% probability that 10 of them are NOT confident that their major would lead to a good job