Answer:
a. EOQ = 1449 units are the optimal number of units of Filters to be produced.
b. I = 1400.7 units is the maximum level of on hand inventory any time.
c. Portion of Uptime = 3.3%
Step-by-step explanation:
Solution:
a.
First of we need to find out the total demand of the filters per year.
D = Demand
D = 200 x 12
Total Demand per year D = 2400 units per year.
Secondly, we need to calculate the production capacity by using the following formula:
PC = Rate of the Production x months in a year x working hours x working days.
PC = 50 x 12 x 6 x 20
PC = 7200 units is the production capacity for a year.
Thirdly, we need to calculate the holding cost by using the following formula:
Holding Cost = Annual interest rate x Production cost per unit.
HC = 0.22 x 2.50
HC = 0.55 is the holding cost
Now, we need to find the modified holding cost as well by using the following formula:
HC' = HC(1-
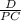 )
)
Where,
D = Total Demand
PC = Production Capacity per year.
Just Plugging in the values, we get:
HC' = 0.55 x (1 -
 )
)
HC' = 0.5317 USD per unit.
Finally, for part a, we need to find the Economic Order Quantity, by using the formula:
EOQ =

Where,
OC = Ordering Cost.
Just plugging in the values:
EOQ =
![\sqrt{(2 * 2400 * [(100+55)]*1.5)/(0.5317) }](https://img.qammunity.org/2022/formulas/business/college/y0poo1jwqjjzm3o21v02qpfnns9rstw924.png)
Hence,
EOQ = 1449 units are the optimal number of units of Filters to be produced.
b.
For this part, firstly, we need to find the inventory at any time:
I = EOQ x (1 -
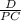 )
)
We already know all the values, so just plug in the value into the above equation to calculate inventory at any time:
I = 1449 x ( 1 -
 )
)
I = 1400.7 units is the maximum level of on hand inventory any time.
c.
For this final part, first we need to find the cycle time as below:
CT =
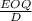
CT = 1449/2400
Hence, the cycle time is:
CT = 0.60375 per year.
Now, we need to find the uptime:
UT =

We already know the values, just plug them in:
UT = 1449/72000
UT = 0.0201 per year
Finally, with all the data collected, we can now calculate the portion of cycle time according to uptime in the production process as follows:
Portion of uptime =

Portion of Uptime = 0.0201/0.60375
Hence,
Portion of Uptime = 3.3%