Step-by-step explanation:
Given info: The Number of turns in the wire is 580 the diameter of
tube is
 and the length of the tube up to which wire is wrapped is
and the length of the tube up to which wire is wrapped is
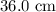 .
.
Formula to calculate the inductance of the coil is,
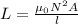
Here,
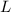 is inductance of the coil.
is inductance of the coil.
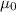 is the permittivity.
is the permittivity.
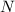 is the number of turns.
is the number of turns.
 is the length up to which wire is wrapped.
is the length up to which wire is wrapped.
 is the cross sectional area of the coil.
is the cross sectional area of the coil.
The expression for the area is,
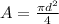
Substitute
![(\pi d^(2))/(4)[tex] for [tex]A](https://img.qammunity.org/2022/formulas/physics/college/uko5n5kwjbvn7sn30zyzi0nv6u0nfzf4oi.png) in equation (1).
in equation (1).
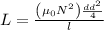
Substitute 580 for
![N, 4 \pi * 10^(-7)[tex] for [tex]\mu_(0), 8.00 \mathrm{~cm}[tex] for [tex]d[tex] and [tex]36.0 \mathrm{~cm}[tex] for [tex]l .](https://img.qammunity.org/2022/formulas/physics/college/sato24tgp0rfki12kko7gscwifvfk9xw8c.png)
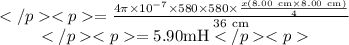
Conclusion:
Therefore, the inductance of the given single conductor wire is
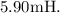
Given info: The rate of increasing current
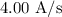 and the inductance of the coil
and the inductance of the coil
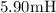 .
.
The generated emf is,
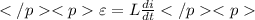
Here,
 is the generated emf.
is the generated emf.
![L[tex] is the inductance of the coil. </p><p>[tex](d i)/(d t)[tex] is the rate of change of current. </p><p>Substitute [tex]5.90 \mathrm{mH}[tex] for [tex]L[tex] and [tex]4.00 \mathrm{~A} / \mathrm{s}[tex] for [tex](d i)/(d t)](https://img.qammunity.org/2022/formulas/physics/college/cg7vcajpmy5rve5j5q5ra7utzyxbcbe8q6.png)
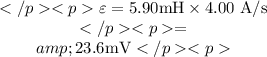
Conclusion:
Therefore, the generated emf is
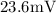 .
.