Answer:
The standard error of the difference in the mean number of fish caught before and after the fire is 0.2153.
Explanation:
Subtraction of normal variables:
When we subtract two normal variables, the standard deviation is the square root of the sum of variances of each variable.
Central Limit Theorem
The Central Limit Theorem estabilishes that, for a normally distributed random variable X, with mean
 and standard deviation
and standard deviation
 , the sampling distribution of the sample means with size n can be approximated to a normal distribution with mean
, the sampling distribution of the sample means with size n can be approximated to a normal distribution with mean
 and standard deviation
and standard deviation
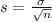 .
.
For a skewed variable, the Central Limit Theorem can also be applied, as long as n is at least 30.
Sample of 195 fishing reports before the fire, the mean catch was 6.3 fish with a standard deviation of 1.6.
The standard error for this sample is:
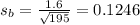
Sample of 143 reports three years after the fire, the mean catch was 7.1 fish with a standard deviation of 2.1.
The standard deviation for this sample is:
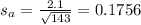
What represents the standard error of the difference in the mean number of fish caught before and after the fire?
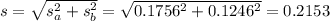
The standard error of the difference in the mean number of fish caught before and after the fire is 0.2153.