Question

It is desired to compare the hourly rate of an entry-level job in two fast-food chains. Eight locations for each chain are randomly selected throughout the country, the selections for each chain being independent. The following hourly rates are recorded:

Chain A 4.25 4.75 3.80 4.50 3.90 5.00 4.00 3.80
Chain B 4.60 4.65 3.85 4.00 4.80 4.00 4.50 3.65
Under the assumption of normality and equal variances, can it be concluded at the 5% significance level that chain A pays more than chain B for the job under consideration?

Answer 1

It can be concluded that at 5% significance level that there is no difference in the amount paid by chain A and chain B for the job under consideration

Step by Step Solution:

The given data are;

Chain A 4.25, 4.75, 3.80, 4.50, 3.90, 5.00, 4.00, 3.80

Chain B 4.60, 4.65, 3.85, 4.00, 4.80, 4.00, 4.50, 3.65

Using the functions of Microsoft Excel, we get;

The mean hourly rate for fast-food Chain A,
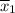`\overline x_1` = 4.25

The standard deviation hourly rate for fast-food Chain A, s₁ = 0.457478

The mean hourly rate for fast-food Chain B,
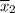`\overline x_2` = 4.25625

The standard deviation hourly rate for fast-food Chain B, s₂ = 0.429649

The significance level, α = 5%

The null hypothesis, H₀:
`\overline x_1` =
`\overline x_2`

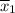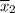
The alternative hypothesis, Hₐ:
`\overline x_1` ≠
`\overline x_2`

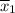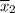
The pooled variance,
`S_p^2`, is given as follows;

`S_p^2 = (s_1^2 \cdot (n_1 - 1) + s_2^2\cdot (n_2-1))/((n_1 - 1)+ (n_2 -1))`

Therefore, we have;

`S_p^2 = (0.457478^2 \cdot (8 - 1) + 0.429649^2\cdot (8-1))/((8 - 1)+ (8 -1)) \approx 0.19682`

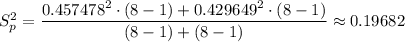
The test statistic is given as follows;

`t=\frac{(\bar{x}_(1)-\bar{x}_(2))}{\sqrt{S_(p)^(2) \cdot \left((1 )/(n_(1))+(1)/(n_(2))\right)}}`

Therefore, we have;

`t=\frac{(4.25-4.25625)}{\sqrt{0.19682 * \left((1 )/(8)+(1)/(8)\right)}} \approx -0.028176`

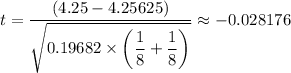
The degrees of freedom, df = n₁ + n₂ - 2 = 8 + 8 - 2 = 14

At 5% significance level, the critical t = 2.145

Therefore, given that the absolute value of the test statistic is less than the critical 't', we fail to reject the null hypothesis and it can be concluded that at 5% significance level that chain A pays the same as chain B for the job under consideration