Question

Over the years, parking has become an issue during spring at MSU as more people bring cars to campus. The waiting time to find a parking spot at Wells Hall parking lot is normally distributed with an average of 9.60 minutes and a standard deviation of 2.60 minutes during peak hours (10 am - 5 pm).

1) What proportion of waiting times are between 8 and 10.8 minutes? Enter your answer to 4 decimal places.
2) What proportion of waiting times are less than 6.8 minutes? Enter your answer to 4 decimal places.
3) You reach Wells Hall parking lot and your class starts in 12 minutes. What is the chance that you are late to class, that is waiting time is at least 12 minutes?
4) Based on your unpleasant experiences in the past you know that your waiting time is in the top 4%. What is the cutoff for the top 4% of waiting times?
5) What is the waiting time for the 30th percentile?

Answer 1

1) 0.4096 = 40.96% of waiting times are between 8 and 10.8 minutes.

2) 0.1401 = 14.01% of waiting times are less than 6.8 minutes.

3) 0.1788 = 17.88% probability that you are late.

4) The cutoff for the top 4% of waiting times is of 14.15 minutes.

5) The waiting time for the 30th percentile is of 8.235 minutes.

Explanation:

Normal Probability Distribution:

Problems of normal distributions can be solved using the z-score formula.

In a set with mean
`\mu` and standard deviation
`\sigma`, the zscore of a measure X is given by:

`Z = (X - \mu)/(\sigma)`

The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the pvalue, we get the probability that the value of the measure is greater than X.

Average of 9.60 minutes and a standard deviation of 2.60 minutes during peak hours.

This means that
`\mu = 9.6, \sigma = 2.6`

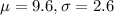
1) What proportion of waiting times are between 8 and 10.8 minutes?

This is the pvalue of Z when X = 10.8 subtracted by the pvalue of Z when X = 8. So

X = 10.8

`Z = (X - \mu)/(\sigma)`

`Z = (10.8 - 9.6)/(2.6)`

`Z = 0.46`

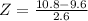
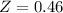
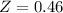`Z = 0.46` has a pvalue of 0.6772

X = 8

`Z = (X - \mu)/(\sigma)`

`Z = (8 - 9.6)/(2.6)`

`Z = -0.62`

`Z = -0.62` has a pvalue of 0.2676

0.6772 - 0.2676 = 0.4096

0.4096 = 40.96% of waiting times are between 8 and 10.8 minutes.

2) What proportion of waiting times are less than 6.8 minutes?

This is the pvalue of Z when X = 6.8.

`Z = (X - \mu)/(\sigma)`

`Z = (6.8 - 9.6)/(2.6)`

`Z = -1.08`

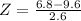
`Z = -1.08` has a pvalue of 0.1401

0.1401 = 14.01% of waiting times are less than 6.8 minutes.

3) You reach Wells Hall parking lot and your class starts in 12 minutes. What is the chance that you are late to class, that is waiting time is at least 12 minutes?

This is 1 subtracted by the pvalue of Z when X = 12. So

`Z = (X - \mu)/(\sigma)`

`Z = (12 - 9.6)/(2.6)`

`Z = 0.92`

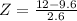
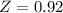
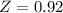`Z = 0.92` has a pvalue of 0.8212

1 - 0.8212 = 0.1788

0.1788 = 17.88% probability that you are late.

4) Based on your unpleasant experiences in the past you know that your waiting time is in the top 4%. What is the cutoff for the top 4% of waiting times?

The cutoff for the top 4% of times is the 100 - 4 = 96th percentile, which is X when Z has a pvalue of 0.96. so X when Z = 1.75.

`Z = (X - \mu)/(\sigma)`

`1.75 = (X - 9.6)/(2.6)`

`X - 9.6 = 1.75*2.6`

`X = 14.15`

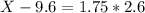
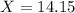
The cutoff for the top 4% of waiting times is of 14.15 minutes.

5) What is the waiting time for the 30th percentile?

This is X when Z has a pvalue of 0.3. So X when Z = -0.525.

`Z = (X - \mu)/(\sigma)`

`-0.525 = (X - 9.6)/(2.6)`

`X - 9.6 = -0.525*2.6`

`X = 8.235`

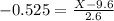
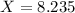
The waiting time for the 30th percentile is of 8.235 minutes.