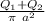Answer:
a) σ =
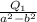 , b) σ =
, b) σ =
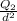 , c) Q_ {total} = Q₁ + Q₂, σ_ {net} =
, c) Q_ {total} = Q₁ + Q₂, σ_ {net} =
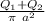
Step-by-step explanation:
a) The very useful concept of charge density is defined by
σ = Q / A
In this case we have a circular disk
The are of a circle is
A = π r²
in this case we have a hole in the center of radius r = b, so
A_net = π r² - π r_ {hollow} ²
A_ {net} = π (a² - b²)
whereby the density is
σ =
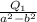
b) The density of the other disk is
σ = Q₂ / A₂
σ =
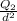
c) The total waxed load is requested by the larger circle
Q_ {total} = Q₁ + Q₂
the net charge density, in the whole system is
σ =
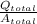
the area is
A_{total} = π a²
since the other circle is inside, we are ignoring the space between the two circles
σ_ {net} =