Question

The thickness of the backfat in pigs is used in evaluating the quality of their flesh for consumption. To compare the backfat thickness of pigs raised on two different diets, an animal researcher randomly sampled a group of pigs raised on Diet 1 and another group raised on Diet 2:

Sample Mean Sample SD Sample Size
Diet 1 3.63 cm 0.29 cm 18
Diet 2 3.37 cm 0.25 cm 18
POOLED SE 0.09
A) After confirming all relevant assumptions, you want to test if the mean backfat thicknesses of the pigs raised on these two diets differs. What is the absolute value of the test statistic?
B) If the critical value for this test is 2.032 (confirm that it is), what would be an appropriate conclusion for this test?
A. An conclusion is not warranted for this test
B. This data provides evidence that mean backfat thickness of pigs on Diet 1 is different from pigs on Diet 2 (p<.05)
C. This data provides no evidence that mean backfat thickness of pigs on Diet 1 is different from pigs on Diet 2 (p<.05)
D. This data provides evidence that diet is independent of backfat thickness (p<.05)
E. There is no evidence that diet is independent of backfat thickness (p>.05)

Answer 1

A) The test statistic is approximately 7.5056

B) E. There is no evidence that diet is independent of backfat thickness

Explanation:

The given data are;

The sample mean for pigs raised on Diet 1,
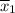`\overline x_1` = 3.63 cm

The sample SD for pigs raised on Diet 1, s₁ = 0.29 cm

The number of pigs in the sample for pigs raised on Diet 1, n₁ = 18

The sample mean for pigs raised on Diet 2,
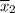`\overline x_2` = 3.37 m

The sample SD for pigs raised on Diet 2, s₂ = 0.25 cm

The number of pigs in the sample for pigs raised on Diet 2, n₂ = 18

The pooled SE = 0.09

A) The test statistic is given by the following formula;

`t=\frac{(\bar{x}_(1)-\bar{x}_(2))}{\sqrt{(s_(1)^(2) )/(n_(1))-(s _(2)^(2))/(n_(2))}}`

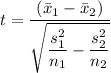
Therefore, we have;

`t=\frac{(3.63-3.37)}{\sqrt{(0.29^(2) )/(18)-(0.25^(2))/(18)}} \approx 7.5056`

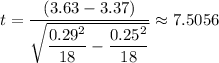
The test statistic, t ≈ 7.5056

B) The degrees of freedom, df = n₁ - 1 = 18 - 1 = 17

At a confidence level of 95%, the critical value is 2.11

Given that the value of the test statistics tic if larger than the critical value, the null hypothesis is rejected and there is a difference in the backfat of the pigs on different diet

Therefore, there is no evidence that diet is independent of backfat thickness