Question

After being rejected for employment, Kim Kelly learns that the Bellevue Credit Company has hired only three women among the last 21 new employees. She also learns that the pool of applicants is very large, with an approximately equal number of qualified men as qualified women. Help her address the charge of gender discrimination by finding the probability of getting three or fewer women when 21 people are hired, assuming that there is no discrimination based on gender.

Does the resulting probability really support such a charge?

Answer 1

0.00071 = 0.71% probability of getting three or fewer women when 21 people are hired. This probability, which is very small, supports the charge of gender discrimination.

Explanation:

For each employee hired, the are only two possible outcomes. Either it is a man, or it is a woman. The probability of a person hired being a man or a woman is independent of any other person. This means that we use the binomial probability distribution to solve this question.

Binomial probability distribution

The binomial probability is the probability of exactly x successes on n repeated trials, and X can only have two outcomes.

`P(X = x) = C_(n,x).p^(x).(1-p)^(n-x)`

In which
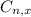`C_(n,x)` is the number of different combinations of x objects from a set of n elements, given by the following formula.

`C_(n,x) = (n!)/(x!(n-x)!)`

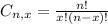
And p is the probability of X happening.

21 new employees.

This means that
`n = 21`

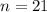
She also learns that the pool of applicants is very large, with an approximately equal number of qualified men as qualified women.

This means that
`p = 0.5`

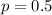
Help her address the charge of gender discrimination by finding the probability of getting three or fewer women when 21 people are hired.

This is

`P(X \leq 3) = P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3)`

`P(X = x) = C_(n,x).p^(x).(1-p)^(n-x)`

`P(X = 0) = C_(21,0).(0.5)^(0).(0.5)^(21) \approx 0`

`P(X = 1) = C_(21,1).(0.5)^(1).(0.5)^(20) = 0.00001`

`P(X = 2) = C_(21,2).(0.5)^(2).(0.5)^(19) = 0.0001`

`P(X = 3) = C_(21,3).(0.5)^(3).(0.5)^(18) = 0.0006`

`P(X \leq 3) = P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3) = 0 + 0.00001 + 0.0001 + 0.0006 = 0.00071`

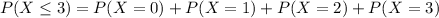
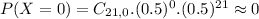
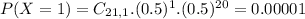
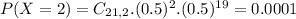
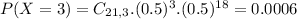
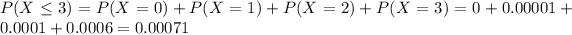
0.00071 = 0.71% probability of getting three or fewer women when 21 people are hired. This probability, which is very small, supports the charge of gender discrimination.