Question

WILL MARK B!
Please I need help I have a quiz

Answer 1

`a) [x: - \infty < x < \infty ]`

`b)[x: - 1]`

`c) [x:- (5)/(3) ]`

`d) [x: 3, 0]`

`e) [x: - (1)/(4) ]`

Answer 2

a) 2x² - x + 3 = x(2x + 1) - 2x

<=> 2x² - x + 3 = 2x² + x - 2x

<=> 3 - x = - x

<=> 3 = 0

=> no solution

b) x/2 - x/3 - x/4 = 1/12

`(6x)/(12) - (4x)/(12) - (3x)/(12) = (1)/(12) \\ \\ ( - x)/(12) = (1)/(12) \\ \\ = > - x = 1 \\ \\ \\ < = > x = 1`

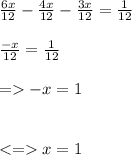
=> the euqation has the solution x = 1

c) |x - 5| = 2|x|

=> x - 5 = 2x

or x - 5 = -2x

<=> x = -5

or 3x = 5

<=> x = -5

x = -5or x = 5/3

d) defined conditions: 2 - x 》 0

<=> x 《 2

we have:

`√(x + 4) = 2 - x \\ < = > x + 4 = (2 - x) {}^(2) \\ < = > x + 4 = {x}^(2) - 4x + 4 \\ < = > {x}^(2) - 5x = 0 \\ < = > x(x - 5) = 0 \\`

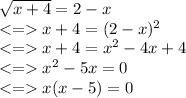
<=> x = 0 (because x 《 2)

e)

`√(5) = \frac{1}{25 {}^(x) } \\ = > 5 = \frac{1}{25 {}^(2x) } \\ < = > 5.25 {}^(2x) = 1 \\ < = > 5.5 {}^(4x) = 1 \\ < = > 5 {}^(4x + 1) = 1 \\ = > 4x + 1 = 0`

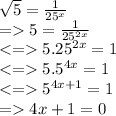
<=> x = -1/4