Question

H(1)= 9

h(n)=h(n−1)⋅(-3)

Find an explicit formula for h(n).

h(n)= ?

​

Answer 1

Given:

`h(1)=9`

`h(n)=h(n-1)\cdot (-3)`

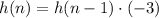
To find:

The explicit formula for h(n).

Solution:

We have,

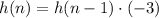`h(n)=h(n-1)\cdot (-3)` ...(i)

It is the recursive formula of a geometric sequence. It is of the form

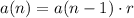`a(n)=a(n-1)\cdot r` ...(ii)

where r is the common ratio.

On comparing (i) and (ii), we get

`r=-3`

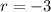
We have,
`h(1)=9` so the first term of the geometric sequence is
`a=9`.

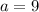The explicit formula for a geometric sequence is:

`h(n)=ar^(n-1)`

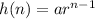
Substitute a=9 and r=-3 to get the explicit formula for the given sequence.

`h(n)=9(-3)^(n-1)`

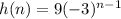
Therefore, the required explicit formula is
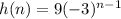`h(n)=9(-3)^(n-1)`.