Answer:
67 monedas de 5, 34 de 10 y 11 de 25.
Explanation:
Representemos el primer enunciado de manera algebraica:
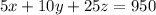 (1)
(1)
Donde:
- x es el numero de monedas de 5
- y es el numero de monedas de 10
- z es el numero de monedas de 25
Ahora, el número de monedas de 10 centavos era el triple de las de 25 centavos y que las de 5 centavos era el doble de las de 10 centavos, se puede representar como:
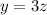 (2)
(2)
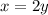 (3)
(3)
Combinado las eacuaciones (1), (2) y (3) tenemos:
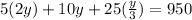
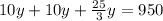
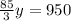
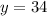
Por lo tanto el valor de x y z seran:
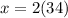
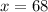
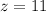
Si ponemos cada valor en la equacion (1), tenemos:
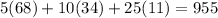
Como el resultado da 955 hay un excedente de 5 pesos, asi que finalmente tendremos.
x = 67
y = 34
z = 11
Espero te haya serrvido!