Given:
Point on straight line = (-6,4)
Gradient = -2
To find:
The equation of the line.
Solution:
Point-slope form: If a line passes through the point
 with slope m, then the equation of the line is
with slope m, then the equation of the line is
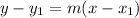
The line passes through the point (-6,4) with slope -2. So, the equation of the line is:
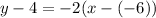
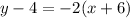
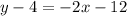
Adding 4 on both sides, we get
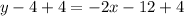

Therefore, the equation of the line is
 .
.