Answer:
The centroid of ∆ABC is (3 , 2).
Step-by-step explanation:
Solution :
Here's the required formula to find the centroid of ∆ABC :
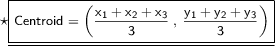
Where :
Substituting all the given values in the formula to find the centroid of ∆ABC
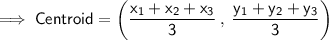
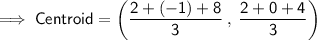
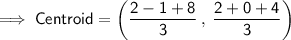
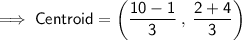
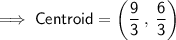
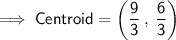

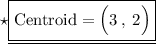
Hence, the centroid of ∆ABC is (3 , 2).
