Question

a) In a simple random sample of 1000 faculty taken among all universities in a country, the number of papers published by the individual sampled faculty in the past year had a mean of 1.1 and an SD of 1.8. Does the Central Limit Theorem say that the distribution of the number of papers published by the individual sampled faculty in the past year is roughly normal

Answer 1

According to the Central Limit theorem, the distribution is roughly normal

Explanation:

The Central Limit Theorem states that for sample sizes above 30 and not withstanding population distribution's shape, the sampling distribution of the sample mean becomes more similar t hat of a normal distribution as the sample size increases;

The size of the sample = 1,000 >> 30

As the sample size approaches infinity, we have;

`z=\frac{\bar{x}-\mu }{(S.D.)/(√(n))}`

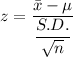
`\overline x` = 1.5

S.D. = 1.8

n = 1000

Assume μ = 1, we get;

`P(x > 1.1):z=(1.1-1 )/((1.8)/(√(1000))) = 1.7568`

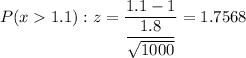
P(z > 1.7568) = 1 - 0.96080 = 0.0392

Therefore, it is very likely that the mean of the population is not larger than the sample mean

Therefore, yes, the Central Limit Theorem say that the distribution of the number of papers published by the individual sampled faculty in the past year is roughly normal