Question

A soda bottling plant uses automated filling machines to fill 2-liter bottles with soda. The plant can produce 8000 bottles of soda in an 8-hour shift. The plant’s quality manager wants to determine how well the process is operating. He takes a sample of 100 bottles from the bottling line and determines that on an average, each bottle contains 2.07 liters of soda, with a standard deviation of 0.06 liters. The specification limits for a bottle of soda are 2.1 liters and 1.9 liters

Answer 1

0.6892 = 68.92% of bottles are within specification.

Explanation:

Normal Probability Distribution:

Problems of normal distributions can be solved using the z-score formula.

In a set with mean
`\mu` and standard deviation
`\sigma`, the zscore of a measure X is given by:

`Z = (X - \mu)/(\sigma)`

The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the pvalue, we get the probability that the value of the measure is greater than X.

On average, each bottle contains 2.07 liters of soda, with a standard deviation of 0.06 liters.

This means that
`\mu = 2.07, \sigma = 0.06`

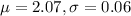
The plant’s quality manager wants to determine how well the process is operating.

To do this, we find the proportion of bottles within specification.

The specification limits for a bottle of soda are 2.1 liters and 1.9 liters

This is the pvalue of Z when X = 2.1 subtracted by the pvalue of Z when X = 1.9. So

X = 2.1

`Z = (X - \mu)/(\sigma)`

`Z = (2.1 - 2.07)/(0.06)`

`Z = 0.5`

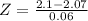
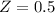
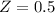`Z = 0.5` has a pvalue of 0.6915.

X = 1.9

`Z = (X - \mu)/(\sigma)`

`Z = (1.9 - 2.07)/(0.06)`

`Z = -2.83`

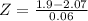
`Z = -2.83` has a pvalue of 0.0023

0.6915 - 0.0023 = 0.6892

0.6892 = 68.92% of bottles are within specification.