Question

The thickness of a flange on an aircraft component is uniformly distributed between 0.95 and 1.05 millimeters. (a) Determine the proportion of flanges that exceeds 1.00 millimeters. Enter your answer in accordance to the item a) of the question statement (b) What thickness is exceeded by 90% of the flanges

Answer 1

a) 0.5 = 50% of flanges exceed 1 millimeter.

b) A thickness of 0.96 millimeters is exceeded by 90% of the flanges

Explanation:

A distribution is called uniform if each outcome has the same probability of happening.

The uniform distributon has two bounds, a and b, and the probability of finding a value higher than x is given by:

`P(X > x) = (b - x)/(b - a)`

The thickness of a flange on an aircraft component is uniformly distributed between 0.95 and 1.05 millimeters.

This means that
`a = 0.95, b = 1.05`

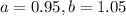
(a) Determine the proportion of flanges that exceeds 1.00 millimeters.

`P(X > 1) = (1.05 - 1)/(1.05 - 0.95) = (0.05)/(0.1) = 0.5`

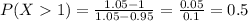
0.5 = 50% of flanges exceed 1 millimeter.

(b) What thickness is exceeded by 90% of the flanges?

This is x for which:

`P(X > x) = 0.9`

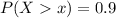
So

`(1.05 - x)/(1.05 - 0.95) = 0.9`

`1.05 - x = 0.9*0.1`

`x = 1.05 - 0.9*0.1`

`x = 0.96`

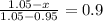
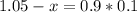
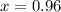
A thickness of 0.96 millimeters is exceeded by 90% of the flanges