Answer:
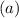
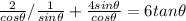
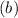
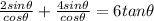
(c) Addition and Quotient identity
Explanation:
Given
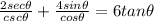 --- The expression missing from the question
--- The expression missing from the question
Solving (a): Write the left hand side in terms of sin and cosine
In trigonometry:

and
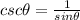
So, the expression becomes:
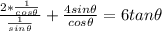
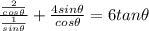
Rewrite as:
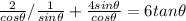
Solving (b): Simplify
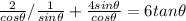
Change / to *
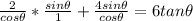
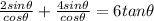
Solving (c): The property used
To do this, we need to further simplify
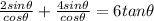
Take LCM
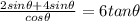
Add the numerator

Apply quotient identity
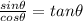
This gives
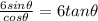
Hence, the properties applied are:
Addition and Quotient identity