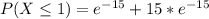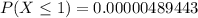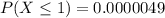Question

Within a computer program, the number of bugs (i.e., coding errors) per lines of code has a Poisson distribution with an average of fifteen bugs per 1,000 lines. a. Find the probability that there will be exactly eight bugs in 1,000 lines of code. b. Find the probability that there will be at least eight bugs in 1,000 lines of code. c. Find the probability that there will be at least one bug in 1,000 lines of code. d. Find the probability that there will be no more than

Answer 1

`P(X=8) = 0.0194`

`P(X \ge 8)= 0.9820`

`P(X \ge 1)= 1`

`P(X\le 1) = 0.0000049`

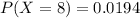
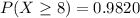
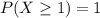
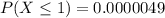
Explanation:

Given

`\lambda = 15`

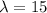
Poisson distribution is given by:

`P(X=x) = (\lambda^x e^(-\lambda))/(x!)`

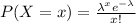
Solving (a): 8 bugs

This implies that:

`x = 8`

So, we have:

`P(X=8) = (15^8 * e^(-15))/(8!)`

`P(X=8) = (783.99418938)/(40320)`

`P(X=8) = 0.0194`

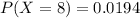
Solving (b): At least 8 bugs

This is represented as:
`P(X \ge 8)`

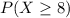
Using complement rule:

`P(X \ge 8)= 1 - P(X<8)`

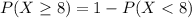
Where

`P(X<8) = P(X=1) + P(X=2) + P(X=3) + P(X=4) + P(X=5) + P(X=6) + P(X=7)`

`P(X<8) = (15^1 * e^(-15))/(1!) + (15^2 * e^(-15))/(2!) + (15^3 * e^(-15))/(3!) + (15^4 * e^(-15))/(4!) + (15^5 * e^(-15))/(5!) + (15^6 * e^(-15))/(6!) + (15^7 * e^(-15))/(7!)`

`P(X<8) = ((15^1)/(1!) + (15^2)/(2!) + (15^3 )/(3!) + (15^4)/(4!) + (15^5)/(5!) + (15^6)/(6!) + (15^7)/(7!)) e^(-15)`

`P(X<8) = (15 + 112.5 + 562.5 + 2109.375 + 6328.125 + 15820.3125 + 33900.6696429) *e^(-15)`

`P(X<8) = 58848.4821429 *e^(-15)`

`P(X<8) = 0.0180`

So:

`P(X \ge 8)= 1 - P(X<8)`

`P(X \ge 8)= 1 - 0.0180`

`P(X \ge 8)= 0.9820`

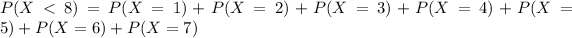
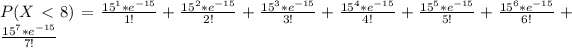
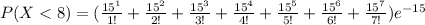
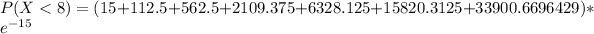
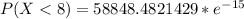
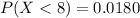
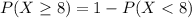
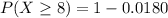
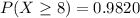
Solving (c): At least 1

This is represented as:
`P(X \ge 1)`

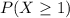
Using complement rule:

`P(X \ge 1)= 1 - P(X<1)`

`P(X<1) = P(X = 0)`

`P(X<1) = (15^0 e^(-15))/(0!)`

`P(X<1) = (e^(-15))/(1)`

`P(X<1) = e^(-15)`

So:

`P(X \ge 1)= 1 - P(X<1)`

`P(X \ge 1)= 1 - e^{-15`

`P(X \ge 1)= 0.99999969409`

`P(X \ge 1)= 1`

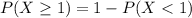
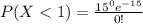
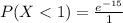
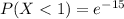
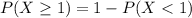
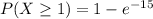
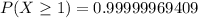
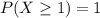
Solving (d): Not more than 1

This implies at most 1.

It is represented as:

`P(X\le 1)`

It is calculated using:

`P(X\le 1) = P(X = 0) + P(X =1)`

`P(X = 0) = e^(-15)`

`P(X=1) = (15^1 * e^(-15))/(1!)`

`P(X=1) = 15 * e^(-15)`

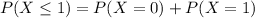
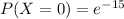
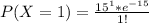
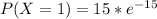
So:

`P(X\le 1) = e^(-15) + 15 * e^(-15)`

`P(X\le 1) = 0.00000489443`

`P(X\le 1) = 0.0000049`