Question

An instructor who taught two sections of statistics last term, the first with 20 students and the second with 30, decided to assign a term project. After all projects had been turned in, the instructor randomly ordered them before grading. Consider the first 15 graded projects. a. What is the probability that exactly 10 of these are from the second section

Answer 1

0.207 = 20.7% probability that exactly 10 of these are from the second section

Explanation:

The students are chosen without replacement, which means that the hypergeometric distribution is used.

Hypergeometric distribution:

The probability of x sucesses is given by the following formula:

`P(X = x) = h(x,N,n,k) = (C_(k,x)*C_(N-k,n-x))/(C_(N,n))`

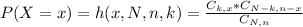
In which:

x is the number of sucesses.

N is the size of the population.

n is the size of the sample.

k is the total number of desired outcomes.

Combinations formula:

`C_(n,x)` is the number of different combinations of x objects from a set of n elements, given by the following formula.

`C_(n,x) = (n!)/(x!(n-x)!)`

In this question:

20 + 30 = 50 total students, which means that
`N = 50`

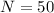
30 students from the second section, which means that
`k = 30`

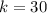
First 15 graded projects, so sample of 15, which means that
`n = 15`

a. What is the probability that exactly 10 of these are from the second section

This is P(X = 10).

`P(X = x) = h(x,N,n,k) = (C_(k,x)*C_(N-k,n-x))/(C_(N,n))`

`P(X = 10) = h(10,50,15,30) = (C_(30,10)*C_(20,5))/(C_(50,15)) = 0.207`

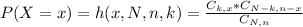
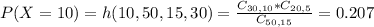
0.207 = 20.7% probability that exactly 10 of these are from the second section