Question

HELP I NEED HELP ASAP

A rectangle has a width represented by the expression-2x+20. The length of the rectangle is 6 more than twice the width. Which expression represents the area of the rectangle?

Answer 1

Rectangular Areas and Perimeters

The perimeter of a rectangle is given by:

`\boxed{\bold{Perimeter = 2 (length + width)}}`

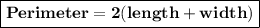
In the problem we have these data:

• Length = a

• Width = -2x + 20

• Perimeter = 6 + 2 (-2x + 20)

We replace the data in the equation of the perimeter:

6 + 2 (-2x + 20) = 2 (a - 2x + 20)

We apply distributive property:

6 - 4x + 40 = 2a - 4x + 40

6 = 2a

6 ÷ 2 = a

3 = a

⇒ Length = 3

The area of ​​the rectangle is given by:

`\boxed{\bold{Area = 2 (length + width)}}`

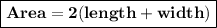
We have these data:

• Length = 3

• Width = -2x + 20

We replace the data in the equation of the area:

Area = (3) (- 2x + 20)

We apply the distributive property and obtain:

Area = -6x + 60

The expression representing the area of ​​the rectangle will be -6x + 60

I hope I've helped!