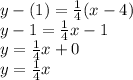Answer:
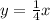
Explanation:
1) First, find the slope of the equation. Use the slope formula
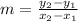 . Substitute the x and y values of the given points into the formula and solve:
. Substitute the x and y values of the given points into the formula and solve:
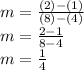
Thus, the slope is
 .
.
2) Now, use the point-slope formula
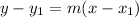 to write the equation in point-slope form (from there we can convert it to slope-intercept). Substitute values for
to write the equation in point-slope form (from there we can convert it to slope-intercept). Substitute values for
 ,
,
 , and
, and
 .
.
Since
 represents the slope, substitute
represents the slope, substitute
 for it. Since
for it. Since
 and
and
 represent the x and y values of one point the line intersects, choose any of the given points (it doesn't matter which one, the end result will be the same) and substitute its x and y values into the formula as well. (I chose (4,1), as seen below.) Then, isolate y to put the equation in slope-intercept form and find the answer.
represent the x and y values of one point the line intersects, choose any of the given points (it doesn't matter which one, the end result will be the same) and substitute its x and y values into the formula as well. (I chose (4,1), as seen below.) Then, isolate y to put the equation in slope-intercept form and find the answer.