Question

A production manager is interested in comparing the precision of two brands of stamping machines. From a random sample of 12 units of output from the Brand A machine, a standard deviation of 15.2 is reported for a quality characteristic. For the Brand B machine, in a sample of 20 units of output, there is a standard deviation of 10.1. Is there sufficient evidence at the 5% significance level to conclude that Brand B machines have a lower variance in quality

Answer 1

There is insufficient statistical evidence at 5% significant level to conclude that Brand B machines have a lower variance in quality

Explanation:

The given parameters are;

The number of units of the sample from Brand A, n₁ = 12 units

The standard deviation of the quality characteristic of Brand A, s₁ = 15.2

The number of units of the sample from Brand A, n₂ = 20 units

The standard deviation of the quality characteristic of Brand B, s₂ = 10.1

The null Hypothesis; H₀; s₁² = s₂²

The alternative Hypothesis; H₀; s₂²< s₁²

The difference of two variance formula;

The F test statistic is given as follows;

`F = (S_1^2)/(S_2^2)`

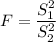
Where;

S₁² = The variance of sample (1) = 15.2² = 231.04

S₂² = The variance sample (2) = 10.1² = 102.01

df₁ = n₁ -1 = 12 - 1 = 11

df₂ = n₂ - 1 = 20 - 1 = 19

From the F table, we have the critical value from the F table = 2.66

`F = (S_1^2)/(S_2^2) = (231.04)/(102.01) \approx 2.265`

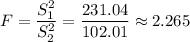
Therefore, given that F ≈ 2.265 is not larger than the critical F for α = 0.05, we do not reject the null hypothesis, and there is sufficient statistical evidence at 5% significance level to conclude that Brand B machines have the same variance in quality as Brand A machines