Question

A consumer products company is formulating a new shampoo and is interested in foam height (in millimeters). Foam height is approximately normally distributed and has a standard deviation of 20 millimeters. The company wishes to test Upper H Subscript 0 Baseline colon mu equals 175 millimeters versus Upper H Subscript 1 Baseline colon mu greater-than 175 millimeters, using the results of n equals 4 samples. Calculate the P-value if the observed statistic is

Answer 1

The p-value of the observed statistic is 0.15866

Explanation:

The given parameters of the system are;

The standard deviation of the foam height, σ = 20 mm

The null hypothesis, H₀; μ = 175 mm

The alternative hypothesis, Hₐ; μ > 175 mm

The number of observations that make the sample, n = 4

The observed statistic,
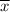`\overline x` = 185

The test statistic is given as follows;

`Z=\frac{\bar{x}-\mu }{(\sigma)/(√(n))}`

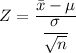
Therefore, we get;

`Z=(185-175 )/((20)/(√(4))) = 1`

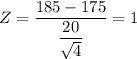
P(Z > 1) = 1 - P(Z < 1) = 1 - 0.84134 = 0.15866

The p-value of the observed statistic = 0.15866