Answer:
a) 0.0498 = 4.98% probability that the number of pieces of junk mail you receive next week will be none at all.
b) 0.1680 = 16.80% probability that the number of pieces of junk mail you receive next week will be exactly four.
c) 0.4232 = 42.32% probability that the number of pieces of junk mail you receive next week will be no more than two.
d) 0.5768 = 57.68% probability that the number of pieces of junk mail you receive next week will be more than two.
Explanation:
We have only the mean, which means that we use the Poisson distribution to solve this question.
In a Poisson distribution, the probability that X represents the number of successes of a random variable is given by the following formula:

In which
x is the number of sucesses
e = 2.71828 is the Euler number
 is the mean in the given interval.
is the mean in the given interval.
You find that you receive on average about 3 pieces of junk mail per week.
This means that

(a) none at all.
This is P(X = 0).

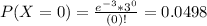
0.0498 = 4.98% probability that the number of pieces of junk mail you receive next week will be none at all.
(b) exactly four.
This is P(X = 4).

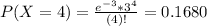
0.1680 = 16.80% probability that the number of pieces of junk mail you receive next week will be exactly four.
(c) no more than two.
This is:


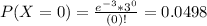
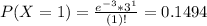
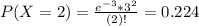
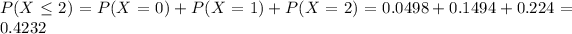
0.4232 = 42.32% probability that the number of pieces of junk mail you receive next week will be no more than two.
(d) more than two
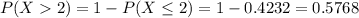
0.5768 = 57.68% probability that the number of pieces of junk mail you receive next week will be more than two.