Answer:
the magnitude of the induced current is 182.86 A.
Step-by-step explanation:
Given;
number of turns, N = 240 turns
cross sectional area of the loop, A = 0.2 m²
uniform magnetic field strength, B = 1.6 T
resistance of the loop, R = 21 ohms
time, Δt = 20.0 ms
The magnitude of the induced emf is calculated as;
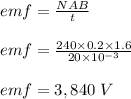
The induced current in the loop is calculated as;

Therefore, the magnitude of the induced current is 182.86 A.