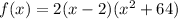Answer:
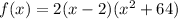
Explanation:
A standard polynomial in factored form is given by:
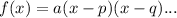
Where p and q are the zeros.
We want to find a third-degree polynomial with zeros x = 2 and x = -8i and equals 320 when x = 4.
First, by the Complex Root Theorem, if x = -8i is a root, then x = 8i must also be a root.
Therefore, we acquire:
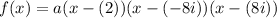
Simplify:

Expand the second and third factors:

Hence, our function is now:
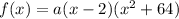
It equals 320 when x = 4. Therefore:
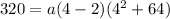
Solve for a. Evaluate:
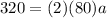
So:

Our third-degree polynomial equation is: