Answer:
The planning value for the population standard deviation is $3750.
Explanation:
Empirical Rule:
The Empirical Rule states that, for a normally distributed random variable:
Approximately 68% of the measures are within 1 standard deviation of the mean.
Approximately 95% of the measures are within 2 standard deviations of the mean.
Approximately 99.7% of the measures are within 3 standard deviations of the mean.
95% confidence interval between $39,000 and $54,000.
This means that $39,000 is two standard deviations below the mean, and $54,000 is two standard deviations above the mean. This means that between $39,000 and $54,000 there are four standard deviations. So
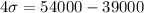
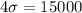
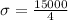
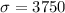
The planning value for the population standard deviation is $3750.