Answer:
Lost Mechanical Power = 7.7565 KW
Head Loss = 26.35 m
Step-by-step explanation:
First, we will find the useful mechanical power used to transport water to the higher reservoir:
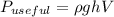
where,
P_useful = Useful mechanical Power = ?
ρ = density of water = 1000 kg/m³
g = acceleration due to gravity = 9.81 m/s²
h = height = 45 m
V = Volume flow rate = 0.03 m³/s
Therefore,
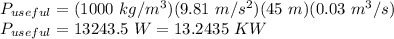
Now, the lost mechanical power will be:
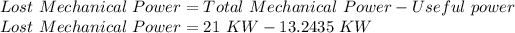
Lost Mechanical Power = 7.7565 KW
Now, for the head loss:
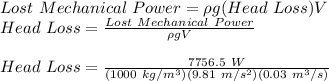
Head Loss = 26.35 m