Question

The formula for any geometric sequence is an = a1 · rn - 1, where a n represents the value of the n th term, a1 represents the value of the first term, r represents the common ratio, and n represents the term number. What is the formula for the sequence -3, -6, -12, -24, ...?

an = -2 · (-3) n - 1
an = 2 · (-3) n - 1
an = -3 · 2 n - 1
an = -3 · (-2) n - 1

Answer 1

C

Explanation:

The formula for any geometric sequence is:

`a_n=a_1\cdot r^(n-1)`

Where aₙ is the value of the nth term, a₁ is the value of the first term, r represents the common ratio, and n represents the term number.

We want the formula for the geometric sequence:

-3, -6, -12, -24, ...

Note that our first term is -3. Hence, a₁ = -3.

Next, each subsequent term is twice the previous term. Hence, our common ratio r = 2.

Therefore, by substitution, we acquire:

`a_n=-3\cdot (2)^(n-1)`

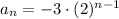
Our answer is C.