Question

Calculus AB Homework, does anyone know how to do this...

Answer 1

(a) f(x) is continuous at x = 1 if the limits of f(x) from either side of x = 1 both exist and are equal:

`\displaystyle \lim_(x\to1^-)f(x) = \lim_(x\to1) (2x-x^2) = 1`

`\displaystyle \lim_(x\to1^+)f(x) = \lim_(x\to1) (x^2+kx+p) = 1 + k + p`

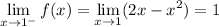
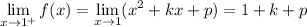
So we must have 1 + k + p = 1, or k + p = 0.

f(x) is differentiable at x = 1 if the derivative at x = 1 exists; in order for the derivative to exist, the following one-sided limits must also exist and be equal:

`\displaystyle \lim_(x\to1^-)f'(x) = \lim_(x\to1^+)f'(x)`

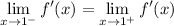
Note that the derivative of each piece computed here only exists on the given open-ended domain - we don't know for sure that the derivative *does* exist at x = 1 just yet:

`f(x) = \begin{cases}2x-x^2 & \text{for }x\le1 \\ x^2+kx+p & \text{for }x>1\end{cases} \implies f'(x) = \begin{cases}2 - 2x & \text{for }x < 1 \\ ? & \text{for }x = 1 \\ 2x + k & \text{for }x > 1 \end{cases}`

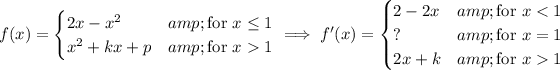
Compute the one-sided limits of f '(x) :

`\displaystyle \lim_(x\to1^-)f'(x) = \lim_(x\to1) (2 - 2x) = 0`

`\displaystyle \lim_(x\to1^+)f'(x) = \lim_(x\to1) (2x+k) = 2 + k`

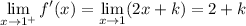
So if f '(1) exists, we must have 2 + k = 0, or k = -2, which in turn means p = 2, and these values tell us that we have f '(1) = 0.

(b) Find the critical points of f(x), where its derivative vanishes. We know that f '(1) = 0. To assess whether this is a turning point of f(x), we check the sign of f '(x) to the left and right of x = 1.

• When e.g. x = 0, we have f '(0) = 2 - 2•0 = 2 > 0

• When e.g. x = 2, we have f '(2) = 2•2 - 2 = 2 > 0

The sign of f '(x) doesn't change as we pass over x = 1, so this critical point is not a turning point. However, since f '(x) is positive to the left and right of x = 1, this means that f(x) is increasing on (-∞, 1) and (1, ∞).

(c) The graph of f(x) has possible inflection points wherever f ''(x) = 0 or is non-existent. Differentiating f '(x), we get

`f'(x) = \begin{cases}2-2x & \text{for }x<1 \\ 0 & \text{for }x=1 \\ 2x+k & \text{for }x>1\end{cases} \implies f''(x) = \begin{cases}- 2 & \text{for }x < 1 \\ ? & \text{for }x = 1 \\ 2 & \text{for }x > 1 \end{cases}`

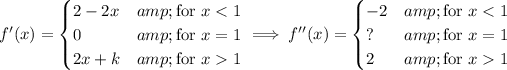
Clearly f ''(x) ≠ 0 if x < 1 or if x > 1.

It is also impossible to choose a value of f ''(1) that makes f ''(x) continuous, or equivalently that makes f(x) twice-differentiable. In short, f ''(1) does not exist, so we have a single potential inflection point at x = 1.

From the above, we know that f ''(x) < 0 for x < 1, and f ''(x) > 0 for x > 1. This indicates a change in the concavity of f(x), which means x = 1 is the only inflection point.