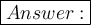
We will use trigonometric identities to solve this. I will use θ (theta) for the angle.
First of all, we know that cotθ = 1/tanθ. This is a trigonometric identity.
We can replace cotθ in the expression with 1/tanθ.
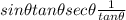
Simplify: 1/tanθ * tanθ = tanθ/tanθ = 1
So now, we have:
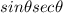
Next, we also know that secθ = 1/cosθ. This is another trigonometric identity.
We can replace secθ with 1/cosθ in our expression.
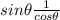
Simplify:
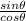
Our third trigonometric identity that we will use is tanθ = sinθ/cosθ.
We can replace sinθ/cosθ with tanθ.
Now we have as our final answer:
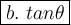
Hope this helps!