Answer:
The cliff is 12.632 meter high.
Step-by-step explanation:
Each stone experiments a free fall motion, that is, an uniformly accelerated motion due to gravity. We construct the respective equations of motion for each stone:
First stone
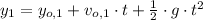 (1)
(1)
Second stone
 (2)
(2)
Where:
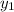 ,
,
 - Final height of the first and second stone, in meters.
- Final height of the first and second stone, in meters.
 ,
,
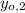 - Initial height of the first and second stone, in meters.
- Initial height of the first and second stone, in meters.
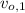 ,
,
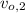 - Initial speed of the first and second stone, in meters per second.
- Initial speed of the first and second stone, in meters per second.
 - Time, in seconds.
- Time, in seconds.
 - Gravitational acceleration, in meters per square second.
- Gravitational acceleration, in meters per square second.
If we know that
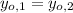 ,
,
 ,
,
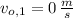 ,
,
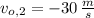 and
and
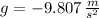 , then we find that time when both stones hit the ground simultaneously is:
, then we find that time when both stones hit the ground simultaneously is:


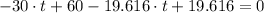
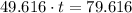
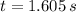
The height of the cliff is:
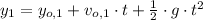
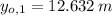
The cliff is 12.632 meter high.