Question

Astronomers observe the motion of four planets that orbit a star similar to the Sun. Each planet follows an elliptical orbit around its star. The astronomers measure each planet's orbital period, as shown in the table.

Planet; Orbital Period (Earth days)
Planet W; 10
Planet X; 640
Planet Y; 80
Planet Z; 270
To determine the distance each planet is from the star, astronomers applied one of Kepler's three laws.
Kepler's first law: The path of each planet around a star is an ellipse, with the star at one focus. Kepler's second law: A planet sweeps out equal areas in equal amounts of time as it revolves around the star.
Kepler's third law: The square of the time for one revolution of a planet is proportional to the cube of the radius of its orbit.
Based on the table, identify the planet that is the farthest distance from the star, and indicate which of Kepler's three laws can be used to justify your answer. Enter your answer in the box provided.​

Answer 1

planet that is farthest away is planet X

kepler's third law

Step-by-step explanation:

For this exercise we can use Kepler's third law which is an application of Newton's second law to the case of the orbits of the planets

T² = (
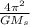`(4\pi ^2)/( G M_s)` a³ = K_s a³

Let's apply this equation to our case

a =
`\sqrt[3]{ (T^2)/(K_s) }`

for this particular exercise it is not necessary to reduce the period to seconds

Plant W

10² = K_s
`a_(w)^3`

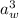
a_w =
`\sqrt[3]{ (100)/( K_s) }`

a_w =
`\frac{1}{ \sqrt[3]{K_s} }` 4.64

Planet X

a_x =
`\sqrt[3]{ (640^3)/(K_s) }`

a_x = \frac{1}{ \sqrt[3]{K_s} } 74.3

Planet Y

a_y =
`\sqrt[3]{ (80^2)/(K_s) }`

a_y = \frac{1}{ \sqrt[3]{K_s} } 18.6

Planet z

a_z =
`\sqrt[3]{ (270^2)/(K_s) }`

a_z = \frac{1}{ \sqrt[3]{K_s} } 41.8

From the previous results we see that planet that is farthest away is planet X

where we have used kepler's third law