Question

In this function, if the value of r were to increase, would the value represented by P also increase or stay the same? Why? Explain your answer using terms such as "rate of growth" and "initial value" in the context of the coin problem.

Answer 1

P will remain the same

Explanation:

Given

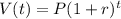`V(t) = P(1 + r)^t` --- Coin value formula [Missing from the question]

Required

What happens to p when r increases

The coin value function is an exponential function which is of the general form:

`y = a(1 + b)^x`

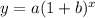
From the given function:
`V(t) = P(1 + r)^t`

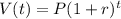
P represents the initial value and r represents the rate

The rate of change (r) and the initial value (P) of a function are both independent, and they do not depend on one another for their values.

An increment or decrement in r will not affect the value of P.

Conclusively, when the rate (r) changes, the initial value (P) will remain the same.