Question

Aight here's the question:

Homeboy Joe is running at 6.65 m/s while Homegirl Jill is running at -1.10 m/s. Home boy Joe and Homegirl Jill hit each other. Homeboy Joe not wanting to be a stage 5 clinger. he makes sure he doesn't hold onto Homegirl Jill after they collide. If Homeboy Joe's mass is 99.5 kg and Homegirl Jill's mass is 68.8 kg. what is Homegir Jill's velocity after they hit if Homeboy Joe's velocity is 2.35?

***Round to the nearest hundredth***

Correct Answer: 5.12

I can't do PEMDAS to save my life can someone show me the correct way to solve with work? ​

Answer 1

`5.12\:\text{m/s}`

Step-by-step explanation:

From the conservation of momentum, the total momentum of the system before and after the collision must be the same. Therefore, let the momentum of Homeboy Joe be
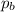`p_b` and let the mass of Homegirl Jill be
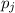`p_j`. We can write the following equation:

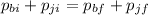`p_(bi)+p_(ji)=p_(bf)+p_(jf)`, where subscripts
`i` and
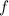`f` represent initial and final momentum respectively.

The momentum of an object is given by
`p=mv`.

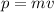Therefore, we have:

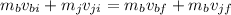`m_(b)v_(bi)+m_(j)v_(ji)=m_(b)v_(bf)+m_(b)v_(jf)` (some messy subscripts but refer to the values being plugged in you're confused what corresponds with what).

Plugging in values, we have:

`99.5\cdot 6.65 + 68.8\cdot (-1.10)=99.5\cdot 2.35+ 68.8\cdot v_(jf)`.

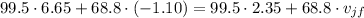Solving, we get:

`v_(jf)=(99.5\cdot 6.65+68.8\cdot (-1.10)-99.5\cdot2.35)/(68.8),\\v_(jf)=5.11875,\\v_(jf)\approx \boxed{5.12\:\text{m/s}}`.

It's important to note that velocity is vector quantity, so the negative velocity assigned to Jill simply implies she is moving at
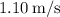`1.10\:\text{m/s}` in the opposite of Joe's direction. After the collision, she is now moving
`5.12\:\text{m/s}` in the same direction that Joe was initially moving, due to Joe's relatively large mass and initial velocity.