Question

A square pyramid has a base with a side length of 6 inches and lateral faces with heights of 11 inches. What is the surface area of the pyramid?

Answer 1

SA = 168 in.²

Explanation:

The surface area is the sum of the area of the base and the areas of the 4 congruent triangular sides.

s = side of the base

h = height of each side

SA = s² + 4(sh/2)

SA = (6 in.)² + 4(6 in.)(11 in.)/2

SA = 36 in.² + 132 in.²

SA = 168 in.²

Answer 2

`\huge\boxed{\sf 168\ in.\²}`

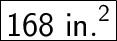
Explanation:

Surface area of the base:

= Length * Length

= 6 * 6

= 36 in.²

Surface Area of 1 Lateral Face:

=
`\sf (1)/(2) (Base * Height)`

Base = 6 inches

Height = 11 inches

= 1/2 (6*11)

= 3 * 11

= 33 in.²

Surface Area of 4 lateral faces:

= 33 * 4

= 132 in.²

Surface Area of the whole pyramid:

= 132 + 36

= 168 in.²

`\rule[225]{225}{2}`

Hope this helped!

~AH1807