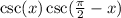Answer:

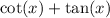
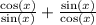
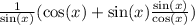

![\csc(x)[(\cos(x)\cos(x))/(\cos(x))+\sin(x)(sin(x))/(\cos(x))]](https://img.qammunity.org/2022/formulas/mathematics/high-school/8h2rsizmikyuhh4d12ifcfsx0vzaisww34.png)
![\csc(x)[(\cos(x)\cos(x)+\sin(x)\sin(x))/(\cos(x))]](https://img.qammunity.org/2022/formulas/mathematics/high-school/amdufrcbwnq4ih3t0e0j4vn93f6cg5itmj.png)
![\csc(x)[(\cos^2(x)+\sin^2(x))/(\cos(x))]](https://img.qammunity.org/2022/formulas/mathematics/high-school/71hf56nq0duo8m56sux1d8x2wfkt247uo7.png)
![\csc(x)[(1)/(\cos(x))]](https://img.qammunity.org/2022/formulas/mathematics/high-school/meili0sff1mu4ke9unmzfneoeb4s6kyl3y.png)
![\csc(x)[\sec(x)]](https://img.qammunity.org/2022/formulas/mathematics/high-school/o1cpf1skncycit6k4nt5oeeza5kk3omtfp.png)
![\csc(x)[\csc((\pi)/(2)-x)]](https://img.qammunity.org/2022/formulas/mathematics/high-school/eqkfpfl0ly8st157vizl450riesxyb5tec.png)
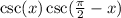
Explanation:
I'm going to use
 instead of
instead of
 because it is less characters for me to type.
because it is less characters for me to type.
I'm going to start with the left hand side and see if I can turn it into the right hand side.

I'm going to use a cofunction identity for the 2nd term.
This is the identity:
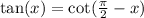 I'm going to use there.
I'm going to use there.
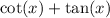
I'm going to rewrite this in terms of
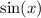 and
and
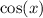 because I prefer to work in those terms. My objective here is to some how write this sum as a product.
because I prefer to work in those terms. My objective here is to some how write this sum as a product.
I'm going to first use these quotient identities:
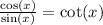 and
and
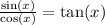
So we have:
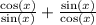
I'm going to factor out
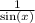 because if I do that I will have the
because if I do that I will have the
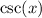 factor I see on the right by the reciprocal identity:
factor I see on the right by the reciprocal identity:
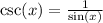
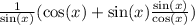

Now I need to somehow show right right factor of this is equal to the right factor of the right hand side.
That is, I need to show
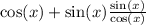 is equal to
is equal to
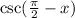 .
.
So since I want one term I'm going to write as a single fraction first:
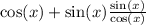
Find a common denominator which is
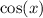 :
:
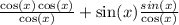
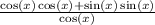
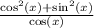
By the Pythagorean Identity
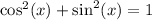 I can rewrite the top as 1:
I can rewrite the top as 1:

By the quotient identity
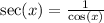 , I can rewrite this as:
, I can rewrite this as:
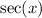
By the cofunction identity
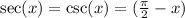 , we have the second factor of the right hand side:
, we have the second factor of the right hand side:
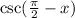
Let's just do it all together without all the words now:

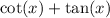
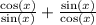
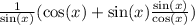

![\csc(x)[(\cos(x)\cos(x))/(\cos(x))+\sin(x)(sin(x))/(\cos(x))]](https://img.qammunity.org/2022/formulas/mathematics/high-school/8h2rsizmikyuhh4d12ifcfsx0vzaisww34.png)
![\csc(x)[(\cos(x)\cos(x)+\sin(x)\sin(x))/(\cos(x))]](https://img.qammunity.org/2022/formulas/mathematics/high-school/amdufrcbwnq4ih3t0e0j4vn93f6cg5itmj.png)
![\csc(x)[(\cos^2(x)+\sin^2(x))/(\cos(x))]](https://img.qammunity.org/2022/formulas/mathematics/high-school/71hf56nq0duo8m56sux1d8x2wfkt247uo7.png)
![\csc(x)[(1)/(\cos(x))]](https://img.qammunity.org/2022/formulas/mathematics/high-school/meili0sff1mu4ke9unmzfneoeb4s6kyl3y.png)
![\csc(x)[\sec(x)]](https://img.qammunity.org/2022/formulas/mathematics/high-school/o1cpf1skncycit6k4nt5oeeza5kk3omtfp.png)
![\csc(x)[\csc((\pi)/(2)-x)]](https://img.qammunity.org/2022/formulas/mathematics/high-school/eqkfpfl0ly8st157vizl450riesxyb5tec.png)