Answer:
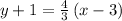
=====================================================
Step-by-step explanation:
The given slope is
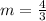 and the line goes through the point
and the line goes through the point
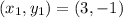
This means
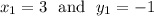
We will plug this information into the point-slope formula below and simplify.
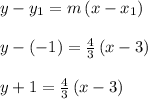
We stop here since your teacher wants the answer in point-slope form. As the name implies, point-slope form is very handy to quickly spot the slope and a point on the line.
If your teacher wanted the answer in slope-intercept form, then you'd solve for y to get it into y = mx+b form.